模式匹配：KMP 算法

发表于2015-09-18字数统计1.3k阅读时长6分

KMP 算法是在给定字符串中检索目标字符串的算法，该算法由 Knuth、Morris 和 Pratt 三人在 Brute-Force 算法的基础上提出的模式匹配改进算法。该算法消除了 Brute-Force 在进行匹配时，只要遇到不相等字符就需要回退到本次比较起始位置的后一个位置继续开始新一轮的比较的缺点，这样的回退就把过程中所有的比较操作的时间付出全部给否定了，KMP 算法则正是需要在匹配失败时，利用之前的匹配结果，再不回退的情况下开始新的一轮比较，KMP 总会将目标字符串向前移动到合适的位置，保证当前指针前的字符串都是匹配的。

KMP 算法执行过程

KMP 算法的核心在于一个 next 数组，这个数组在匹配失败时指明了字符串前移的位数，后面我们专门用一小节来讨论 next 数组的计算。现在我们以字符串 BBC ABCDAB ABCDABCDABDE 来演示用 KMP 的算法查找字符串 ABCDABD 的执行过程，并假设已经有了一个计算好了的 next 数组：

A B C D A B D
-1 0 0 0 0 1 2

那么整一个匹配流程如下：

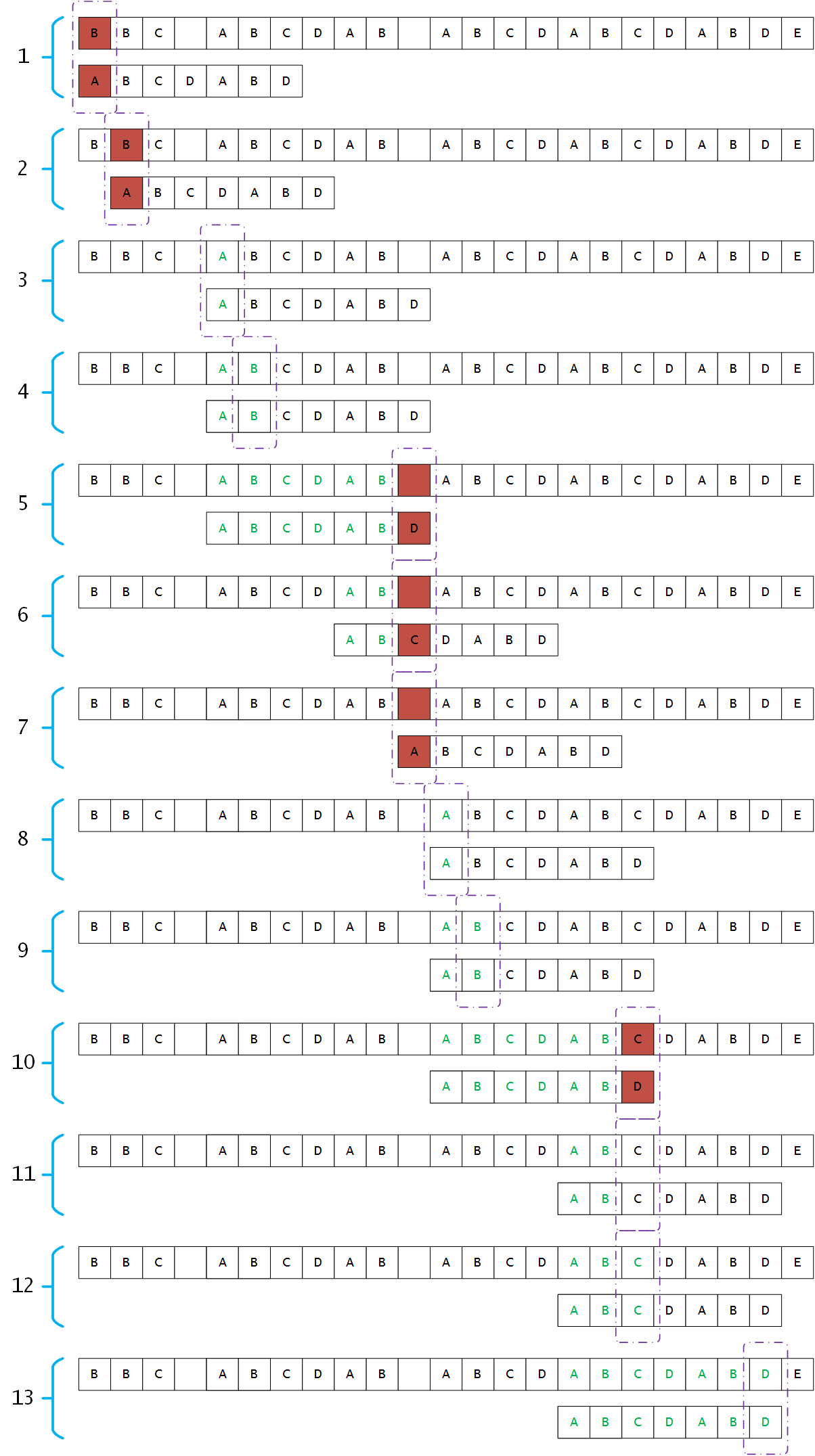
image

如上图所示，我们令原字符串为 txt，目标字符串为 pat，i 为 txt 的指针，j 为 pat 的指针，一开始 i = 0, j = 0，开始匹配过程：

  1. 图 1 所示，不匹配中则 i++；
  2. 图 2 所示，仍然不匹配，i++；
  3. 图 3 所示，继续比较直到第 1 个字符匹配，i++，j++；
  4. 图 4 所示，继续比较，匹配，i++, j++；
  5. 图 5 所示，遇到不匹配，此时需要根据 next 数组重新计算 j 的值，j = next[j]，即 j = next[6] = 2；
  6. 图 6 所示，此时 i=10，j=2，继续比较，不匹配，根据 next 数组重新计算 j 的值，j = next[j] = next[2] = 0；
  7. 图 7 所示，此时 i=10，j=0，继续比较，不匹配，j=0 时，如果不匹配，则直接 i++ 即可；
  8. 图 8 所示，此时 i=11, j=0，匹配，i++，j++；
  9. 图 9 所示，匹配，i++，j++；
  10. 图 10 所示，遇到不匹配，此时 i=17，j=6，因为 j>0，所以需要依据 next 重新计算 j 值，j=next[j] = next[6]=2；
  11. 图 11 所示，比较 text[i=17] 和 pat[j=2]，匹配， i++，j++，如图 12；
  12. 图 13 所示，全部匹配，本次查找完成。

由上面的过程，我们可以总结一下，KMP 算法的下标设置逻辑为：

1
2
3
4
5
6
7
8
if(txt[i] == pat[j]) {
    i++;
    j++;
} else if(j == 0) {
    i++;
} else{
    j = next[j];
}

算法的 java 实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * KMP 检索
 * 如果未检索到则返回 -1
 *
 * @param haystack 原字符
 * @param needle 目标字符
 * @return
 */
public static int search(String haystack, String needle) {
    int lenHay = haystack.length(), lenNeed = needle.length();
    if (lenNeed > lenHay) {
        // 肯定不存在，直接返回 -1
        return -1;
    }
    if (lenNeed == 0) {
        // 查找空白字符串始终返回 0
        return 0;
    }
    int i = 0, j = 0;
    int[] next = next(needle);  // 计算next数组
    while (i < lenHay && j < lenNeed) {
        if (haystack.charAt(i) == needle.charAt(j)) {
            // 匹配
            i++; j++;
        } else if (j == 0) {
            // 不匹配，但j=0，直接递增i
            i++;
        } else {
            // 不匹配，但是已经匹配了一些字符，依据next数组重新计算j
            j = next[j];
        }
    }
    if (j == lenNeed) {
        // 说明匹配到了，返回下标
        return i - lenNeed;
    }
    return -1;
}

next 数组的计算方法

next 数组计算的理论基础

next 数组是 KMP 算法的核心所在，next 数组的计算可以由如下公式表示：

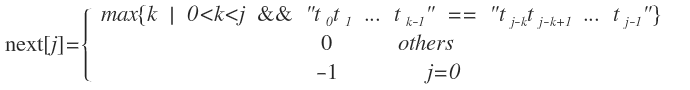
image

上述公式所要表达的意思是，next[j] 的值等于在 0<k<j 的范围内存在一个 k 值将字符串截成两段，且前半段等于后半段，满足这样条件的最大 k 值就是 next[j] 的值。

next 数组的算法设计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * 计算 next 数组
 *
 * @param needle
 * @return
 */
private static int[] next(String needle) {
    int[] next = new int[needle.length()];
    next[0] = -1; // 首字母的next值始终为-1
    int k = -1;
    for (int i = 1; i < needle.length(); ) {
        if (k == -1 || needle.charAt(i - 1) == needle.charAt(k)) {
            next[i] = ++k;
            i++;
        } else {
            k = next[k];
        }
    }
    return next;
}

算法执行流程如下：

image

如果是手动计算，且目标字符串不是很长的情况下，可以采用如下方式计算 next 数组，即 前缀后缀法 ，先来对前缀和后缀下一个定义，假设我们有一个单词 “bread”，那么该单词的前缀有 b, br, bre, brea，同理后缀有 read, ead, ad, d，那么对于之前的字符串 ABCDABD 则计算结果如下：

字符串 前缀 后缀 最长公共字符串 最长公共字符串长度
A 空 空 空 0
AB A B 空 0
ABC A, AB BC, C 空 0
ABCD A, AB, ABC BCD, CD, D 空 0
ABCDA A, AB, ABC, ABCD BCDA, CDA, DA, A A 1
ABCDAB A, AB, ABC, ABCD, ABCDA BCDAB, CDAB, DAB, AB, B AB 2
ABCDABD A, AB, ABC, ABCD, ABCDA, ABCDAB BCDABD, CDABD, DABD, ABD, BD, D 空 0

我们只需要将最后一列的值平放（如下表格第二行），然后整体向右移动一格，首位置为 -1，就可以得到 next 数组（如下表格第三行）：

A B C D A B D
0 0 0 0 1 2 0
-1 0 0 0 0 1 2